Cómo calcular matrices y no morir en el intento.
Saludos!
Le doy la bienvenida a mi blog de Matemáticas, en el que me dedicaré a resolver diversos ejercicios relacionados con el temario de 2º Bachillerato. Espero que este blog sea de gran ayuda a todo aquel quien quiera aumentar sus conocimientos matemáticos.
Sin más dilación, comencemos con el primer tema.
- Resolución de problemas matriciales. Teorema de Rouché-Fröbenius.
Muchos de los ejercicios de ecuaciones con dos incógnitas o más tienen también introducido un parámetro a. el objetivo de dichos ejercicios es el estudio de las soluciones dependiedo del valor que tome a.
Pongamos un ejemplo: consideremos un sistema de ecuaciones de incógnitas x, y, z, como el siguiente:
Como podemos ver, este sistema tiene introducido el parámetro a. En el ejercicio se nos pide sacar los valores de las tres incógnitas dependiendo de lo que vale a.
Pero claro, no sabemos si este sistema tiene o no solución. Para saber al menos si este sistema es compatible o no, formaremos una matriz con las ecuaciones del ejercicio:
Ahora bien, ¿cuándo un sistema es compatible? Según el teorema de Rouché-Fröbenius, un sistema de ecuaciones es compatible cuando el rango de A es igual al rango de A*, y si no lo es, dicho sistema no tendrá solución. Por ello, comenzaremos calculando el rango de A y después el rango de A*.
Para calcular el rango yo siempre intento empezar por el menor posible, que siempre es el rango uno. Para quienes aún tengan dudas, el rango se averigua tomando determinantes de la matriz de menor a mayor orden. Si al menos uno e los determinantes no se anula, el rango tendrá el mismo valor que el orden de la matriz tomada para hacer el detrminante.
Tomando un ejemplo del ejercicio, si tomo un determinante de orden 2x2 y me da un número distinto de 0, la matriz A al menos será de orden 2:
Como podemos ver, el determinante de orden 2 es nulo, pero no podemos confirmar si el rango de la matriz el menor que dos hasta que todos los determinantes de orden 2 nos den 0, y para ello habría que calcular otros 5 determinantes más. Además de ser una tarea larga, no nos proporcionaría mucha información, pues todos los determinantes se anularían dependiendo de los valores de a. Para quen nos tome menos tiempo calcular los valores de a para los que el determinante se anula, procederemos a calcular el determinante de orden 3:
Aquí podemos ver que los valores de a que anulan el determinante de rango 3 son a=0 y a=-1. Dichos valores harán que el rango de nuestra matriz sea menor que 3, pero no sabemos con certeza si el con esos valores el rango será 2 o 1, por lo que se csustituirá a por cada uno de los valores en la matriz A y se verá el número de filas independientes que hay:
En ambos casos el número de filas/columnas independientes es 2, por lo que el rango para a=0 y a=-1 siempre será 2 en la matriz A (la primera vez cometí un error y en vez de poner a=-1 puse a=1, por lo que los resultados fueron distintos, asi que prestad mucha atención con los signos).
Ahora utilizremos los mismos valores en A* para comprobar si el rango de la matriz ampiada varía respecto la matriz A. Si lo hace, el sistema es incompatible y no tendrá solución, pero si no, entonces el sistema será compatible y tendremos que ver si el sistema es determinado o indeterminado:
Para a=0, el rango de A* sigue siendo el mismo que el de A, por lo que es un sistema compatible, pero al ser el rango menor que el número de incógnitas, es un sistema indeterminado, por lo que hay que añadir parámetros al sistema. El número de parámetros a introducir se determina restando al número de incógnitas el rango de la matriz. En este caso solo tenemos que introducir un parámetro lambda (ʎ). El sistema se verá determinado por el valor de ʎ.
Ahora se hará el mismo proceso para a= -1:
Aquí, por lo contrario, el rango de A* aumenta en 3, por lo que no es igual al rango de A. Por lo tanto, es un sistema incompatible para a=-1.
Lo más importante de los ejercicios con matrices es cuidar los signos y no equivocarse al hacer los cálculos, pues el más absurdo de lo erores puede llevar a tener todo el ejercicio mal.
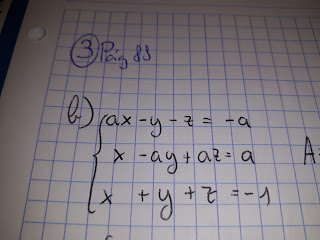







Extraordinario análisis de todo el proceso de discusión y resolución. De hecho solo faltaría un ejercicio para recordar la regla de Cramer en la resolución cuando n=r y det (A) distinto de cero. Solo indicar que no podemos preguntarnos por la compatibilidad de una matriz, sino del sistema en sí. ¡Enhorabuena!
ResponderEliminarMuchas gracias por mirar mi blog! Pronto publicaré una entrada que hable en profundidad de la regla de Cramer.
Eliminar